Breadth First Search

This is an easy and small guide to Breadth First Search. This post does not have the entire code mentioned (although there is a link to the code in the end). The motive is to make you familiar with the concepts and the procedure.

It is recommended to try writing the code on your own.

 

What is Breadth First Search?

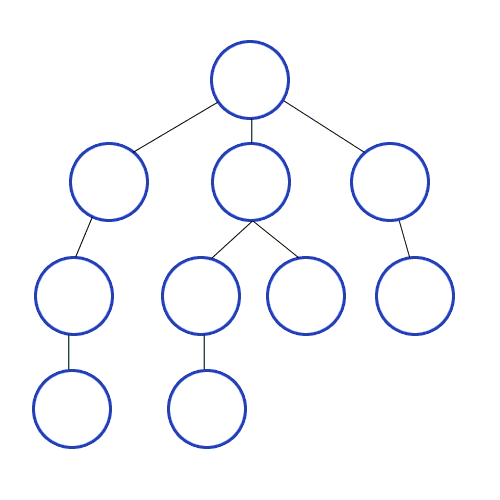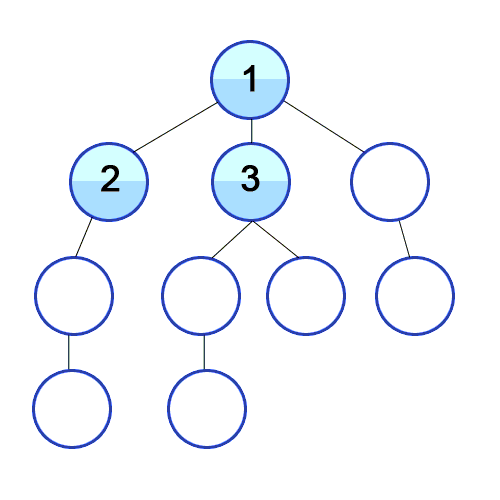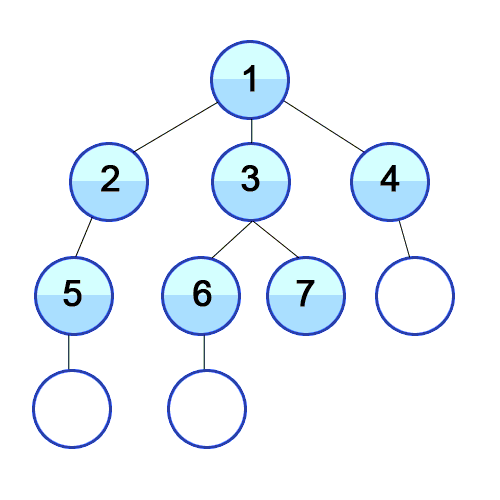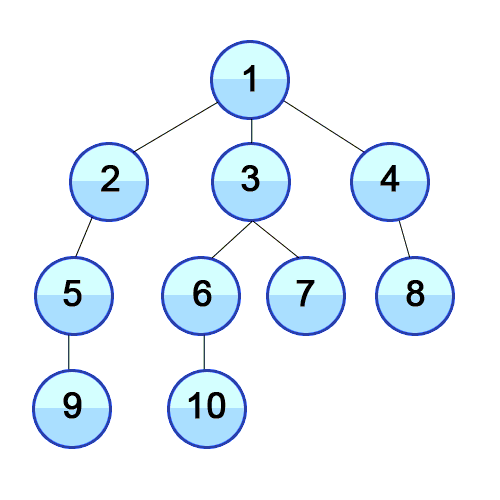
Breadth First Search is a method of traversing a tree or a graph such that it starts with the root/source node and first visits all its neighbors and then continues the same on other nodes.

How do you implement BFS?

1. Keep a visited array to keep track of visited nodes, mark it false for every node except the root/source.
2. Push the node into the queue.
3. Mark it as visited.
4. While queue is not empty, store and print the front of queue 'f' and dequeue.
5. Visit the neighbors of the 'f' and enqueue them if they have not been visited already.
6. Repeat 4-6.

GIF by: commons.wikimedia.org

Why Queue?

Because queue allows us to add and remove the items easily. The important part is that the removed item will be the one which has been enqueued for longest period. This behavior of Queue is called First In First Out (FIFO).

Push/Enqueue

The method to insert an element into the queue. If you're using an array to make the queue, simply insert an element at the end.

GIF by: tutorial4us.com

Pop/Dequeue

The method to delete an element from the queue. If you've implemented queue using array, just remove the first element from the array following FIFO.

GIF by: tutorial4us.com

Front

The method that should return the front end of the queue i.e. the element that should be popped out next.

Empty

The method that should return true if queue is empty, false otherwise.

Uses

1. Finding the shortest path between two nodes in a graph.
2. Ford–Fulkerson method for computing the maximum flow in a network.
3. Testing bipartiteness of a graph.

That is all about Breadth First Search.

Looking for the entire code? See here for C++ solution implemented using STL. {O(V+E)}

Minimum Binary Heap

This is an easy and small guide to minimum binary heap. This post does not have the entire code mentioned (although there is a link to the code in the end). The motive is to make you familiar with the concepts and the procedure.

It is recommended to try writing the code on your own.

What is a minimum binary heap?
A binary tree which follows:

• Heap property : Every parent node should be smaller than its children.
• Shape property : The binary heap should be a complete binary tree.

What operations can you perform on a minimum binary heap?

• Insert : Insert an element in the minimum binary heap. {O(log(n))}
• Delete : Delete an element from the minimum binary heap. {O(log(n))}
• Extract-min : Extract the minimum element from the minimum binary heap. {O(1)}

 
Cascade up

Cascading up means taking up the inserted element to its correct position such that none of the properties of a minimum binary heap are violated. This is also known as bubble-up, percolate-up, sift-up, trickle-up or heapify-up.

1. If the element is smaller than its parent, swap the parent and the child.
2. Continue the process until the element is placed at right position. 

 Insert

For inserting an element in a minimum binary heap, all you got to do is follow these two rules:

1. Insert the element in the end of the tree.
2. Cascade up the element until it is smaller than its parent.

GIF by: algorithms.tutorialhorizon.com

Cascade down

Cascading down is just the opposite of cascade up. This is also known as bubble-down, percolate-down, sift-down, trickle down or heapify-down.

1. Check which of the children of the element is smaller.
2. If the element is greater than the smaller child, swap the element and the child.
3. Continue the process such that the heap follows the two properties.

 

Delete

For deleting an element from a minimum binary heap:

1. Find out the index 'i' of the element.
2. Swap the element with the last node 'n' in the tree.
3. Delete the last element of the tree.
4. Cascade down the node 'n' (now at index 'i') until it is greater than its children.

 

GIF by: algorithms.tutorialhorizon.com

 

 

Extract-min

 

We're always maintaining the two properties of minimum binary heap at the time of insertion as well as deletion. This leaves us to an O(1) solution for extracting the minimum element of the heap.
Guesses?
Yes! Just return the root of the heap.

But, what if you wish to extract the minimum element one after the other?

1. Save the root of the tree 'r'.
2. Swap the root with the last element of the tree.
3. Delete the last element of the tree.
4. Perform Cascade down on now root.
5. Return 'r'.

Uses

• Implementing priority queue
• Heap Sort
• Implementing Dijkstra's algorithm in O(E*log(V))

That is all about minimum binary heap. Similarly, you can do maximum binary heap.

Looking for the entire code? See here for C++ solution.