Breadth First Search

This is an easy and small guide to Breadth First Search. This post does not have the entire code mentioned (although there is a link to the code in the end). The motive is to make you familiar with the concepts and the procedure.

It is recommended to try writing the code on your own.

 

What is Breadth First Search?

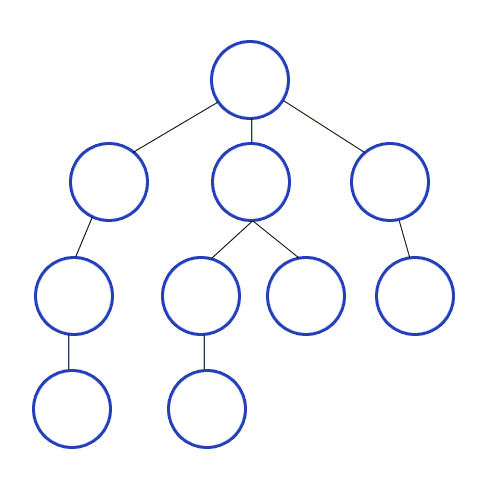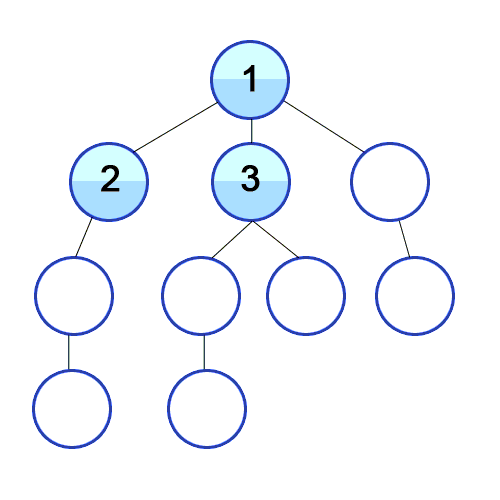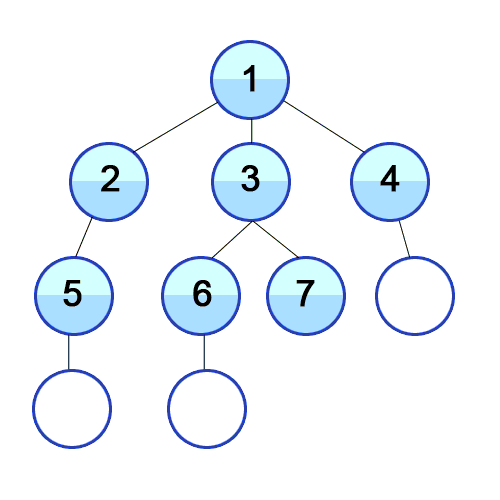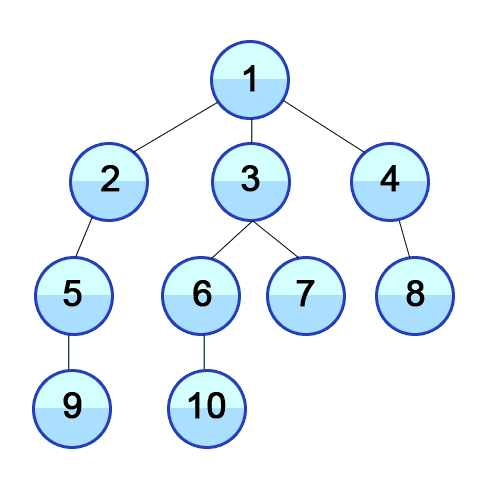
Breadth First Search is a method of traversing a tree or a graph such that it starts with the root/source node and first visits all its neighbors and then continues the same on other nodes.

How do you implement BFS?

1. Keep a visited array to keep track of visited nodes, mark it false for every node except the root/source.
2. Push the node into the queue.
3. Mark it as visited.
4. While queue is not empty, store and print the front of queue 'f' and dequeue.
5. Visit the neighbors of the 'f' and enqueue them if they have not been visited already.
6. Repeat 4-6.

GIF by: commons.wikimedia.org

Why Queue?

Because queue allows us to add and remove the items easily. The important part is that the removed item will be the one which has been enqueued for longest period. This behavior of Queue is called First In First Out (FIFO).

Push/Enqueue

The method to insert an element into the queue. If you're using an array to make the queue, simply insert an element at the end.

GIF by: tutorial4us.com

Pop/Dequeue

The method to delete an element from the queue. If you've implemented queue using array, just remove the first element from the array following FIFO.

GIF by: tutorial4us.com

Front

The method that should return the front end of the queue i.e. the element that should be popped out next.

Empty

The method that should return true if queue is empty, false otherwise.

Uses

1. Finding the shortest path between two nodes in a graph.
2. Ford–Fulkerson method for computing the maximum flow in a network.
3. Testing bipartiteness of a graph.

That is all about Breadth First Search.

Looking for the entire code? See here for C++ solution implemented using STL. {O(V+E)}